Использование динамических геометрических моделей

Подвижные геометрические модели в настоящее время широко используются в преподавании геометрии при открытии понятий, теорем и доказательств. Например, для демонстрации смежных, вертикальных углов, высот, медиан, биссектрис треугольника, параллелограмма, с помощью моделей удобно иллюстрировать движения на плоскости (поворот, параллельный перенос, осевую и центральную симметрию). Гораздо реже используются подвижные модели при изучении различных зависимостей между сторонами и углами треугольника, между величинами проекций и наклонных и т. п. Это изучение чаще всего ведется статично, т. е., рассматривается один частный случай, который характеризуется определенным чертежом. В сознании школьника вместо великого разнообразия случаев, которые описывает изучаемая зависимость, нередко запечатлевается ее «фотография» — застывший неподвижный чертеж. Создается своего рода противоречие между закономерностью общего характера и конкретным чертежом, который вынужден показывать один из частных случаев этой зависимости. Такое положение чревато многочисленными ошибками учеников.

Изображая вместо произвольной фигуры ее частный вид, ученик сам создает себе помехи в решении задач, ибо он невольно пользуется теми особенностями чертежа, которые не входят в условие задачи.

Например, изображая вместо произвольного прямоугольного треугольника равнобёдренный прямоугольный треугольник, ученик нередко использует при решении задачи навеянное чертежом дополнительное условие: острые углы треугольника равны 45°.

По-видимому, возникновению таких серьезных логических ошибок (неверное обобщение) содействует неправильная постановка преподавания геометрии. Иногда учителя, используя при доказательстве чертеж к теореме, не останавливаются на условиях, допускающих обобщение, и ученики невольно усваивают такое «правило»: по одному чертежу можно судить об общих закономерностях. Естественно поэтому, что при решении задач они стремятся брать наиболее «удобные» случаи. Конечно, говоря об условиях, позволяющих высказать общий вывод при рассмотрении одного чертежа, мы в известной мере нейтрализуем стремление учеников к «удобным» случаям. Но этого мало: необходимо также устранять причины, приводящие к ошибкам.

Как показал опыт, результаты в этом отношении обеспечивает изучение планиметрических зависимостей на подвижных моделях своего рода «подвижных чёртежах».

У многих учащихся отсутствует правильное представление о размерах углов. Говоря об угле в 30°, чертится угол в 50° и т. п. Недостаток глазомера, отсутствие навыка в обращении с ходовыми углами значительно осложняет работу по решению задач, а также тормозит дальнейшую практическую деятельность учащихся.

Для развития у учащихся правильных навыков рекомендуется во время изучения углов, построения их, вывесить в классе на небольшой срок (неделю) образцы часто встречающихся в практике углов: 30°, 45°, 60°, 135°. (см. рис. 4.)

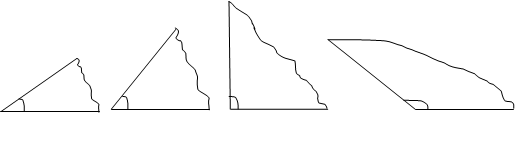
Рис. 4. Образцы часто встречающихся углов

Модели могут быть двух типов: деревянные и картонные.

Ученику дома предлагается изготовить набор небольших моделей различных углов, наклеить их на листе, сделать надписи, поместить в конверт.

Интерес учащихся 7 класса вызывает планиметрическая модель, которая иллюстрирует доказательство теоремы о сумме внутренних углов треугольника.

Углы 1 и 3 треугольника подвижные. Для того чтобы учащиеся выдвинули гипотезу о сумме углов треугольника, учитель эти углы разворачивает на подвижной модели, так как показано на рис. 5

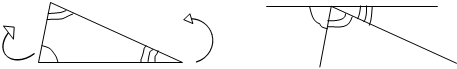
Рис. 5. Модель разворота подвижных углов

При изучении свойства хорды: хорда, не проходящая через центр круга, меньше диаметра, проведенного в том же круге.

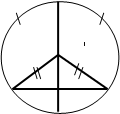
Рис. 6. Модель для изучения свойств хорды

Можно использовать следующую подвижную модель. Модель представляет собой лист картона, на котором начерчена окружность. Вдоль дуги АВD может передвигаться точка В (пуговица) (рис.6). При движении точки В по дуге окружности образуются различные треугольники, обладающие одной общей особенностью, - две стороны (радиусы) не меняют своей длины. Вспоминая свойство отрезка, приходим к выводу, что любая хорда, не проходящая через центр круга, меньше его диаметра. На модели, кстати, видно, почему приходится вводить ограничение «не проходящая через центр круга». В этом случае ломаная АОВ выпрямляется и свойство отрезка применить уже нельзя.

Другие статьи:

Предлагаемые методики для формирования навыков общения у детей с ОНР
Невербальные и вербальные средства общения К невербальным средствам общения относятся: мимика, пантомимика, жесты. Они реализуются в процессе подготовки к драматизации. Именно она имеет эффект и позволяет формировать понимание социальных причинно-следственных ...

Правила семейного воспитания и семейной педагогики
За длительную историю существования семьи накоплено чрезвычайно много наблюдений за воспитанием детей; из них вытекают важные выводы, которые могут быть условно классифицированы как общие закономерности воспитания детей в семье. И хотя они еще не имеют призна ...